First, watch this.
Ridiculous, right? This is a record-breaking moment in the history of a game show that has been on TV since 1956. It’s also a perfect moment to take a look at some game probability as we determine exactly how ridiculous this moment actually is.
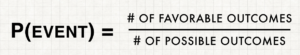Let’s start with Wilbert. Determining the probability of an event occurring requires us to create a pretty simple ratio. On bottom of the fraction are the number of possible outcomes in a situation. On top, the number of favorable outcomes. In this case, we want to find out the number of possible spins of the wheel and the number of ways to get $1.00.
How many possible outcomes are there? There are twenty different spaces on the Wheel, starting at 5 cents and increasing by 5 all the way to $1.00. Your first spin can have any of those twenty results, as can your second spin. However, you only get a second spin if you don’t land on $1.00 the first time. There are 19 ways to get a second spin, and a second spin has 20 different results. We call this the sample space—the group of possible outcomes.
Okay, so how do you get a $1.00? You can either spin it on your first go, or get a total of $1.00 by adding up to spins. If your first spin is 15¢, the only way to get a dollar is with 85¢. 30¢ has to match with 70¢. For each spin, there’s only one possible second spin that nets $1.00 total. Which means there are twenty different favorable outcomes that lead to $1.00. Notice here a trick about probability: we consider 35¢ + 65¢ to be a different outcome than 65¢ + 35¢. Order matters.
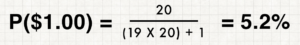
So, not significantly different than rolling a 20 on a d20. But it didn’t just happen once… it happened five times in a row. What are the odds of that? Here’s a moment when you often stump students in a high school probability class (Hi there, former students! –Rich). There are five of them… maybe we should multiply by five? But that makes it more likely that the event occurs, which is wrong. So then maybe the next step is to divide by five… this is the point where I put an X next to the test answer, hope the next one is better, and plan to have a brief discussion about how probabilities are always horribly unintuitive.
When it comes down to it, the right answer is to build a probability tree. When we do this, we can start to put together the actual solution. In probability terms, this is a then question, as in event A occurs, then event B occurs. In then problems, we multiply the probabilities of each outcome together. Which means the odds of these five $1.00 spins happening in a row is roughly one in two and a half million.
How many stars are there in the sky? Would you believe that you only see between 2,500 and 5,000 that are visible to the naked eye at any one time? Think about one star in that vast expanse. One in two and a half million is another few orders of magnitude entirely. So, as much as I enjoy watching Drew Carey’s impersonation of Bob Barker, I’m not planning to see a Showcase Showdown like this one ever again.