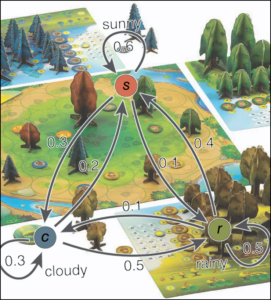
This is the Markovian expansion to Photosynthesis I’m looking for!
After writing last week about random paths and probability, Dave Chalker mentioned on Twitter that this idea reminded him of Markov Chains. In fact, a random path is one of the simplest examples of a Markovian system: given the present state of the system, knowledge of the past is unnecessary to predicting the future. In a random path, each of the past turns aggregate together to describe my current status. However, once I know where I am, I no longer need to remember where I was in each of those past moments! In a sense, this path has achieved a state of “memorylessness.” It didn’t take long to develop the question that would apply this observation to games.
Can games be Markovian? If so, what does that look like?
Let’s parse that out a bit. In a game theoretic way, I describe games as a series of atomic decisions, and a strategy as making choices to achieve a particular goal. To say that a game is Markovian would mean that I can theoretically erase my memory after each turn—I should be able to look at the game board and determine the optimal play without knowing the choices I made in previous turns.
For example, say someone asks me to take over for them in a game of Candyland. I glance at the board to find out the current state of the game. I’m on a blue space, and I’m in third place. Do I need to look back through the discard pile to evaluate what to do on my turn? Absolutely not. I just draw a card and move my piece a little farther down the track towards Candyland.
On the other hand, we’ve got Texas Hold’em. In a single hand of Poker, I have to continually judge everything that has happened up to the moment I take my turn. Do I think that someone’s bet signifies that they’ve made their hand? Or does probability lead me to believe they’re bluffing? What new cards have come out, giving me new information and new chances of making my own hand?
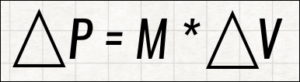
Yes, the letter “P” does not appear in the word “Momentum.” No, I don’t get it either.
Clearly, there is some kind of spectrum here, so let’s quickly go back to school and talk about momentum. Just to cover some introductory physics, we state that momentum is a quantity of motion, determined by the product of mass and velocity. We also know that velocity is a result of an object being accelerated by an initial force. When we try to translate that idea in terms of games, we could say that a gain in momentum is the result of a successful strategy being played out over multiple turns.
So, can you gain momentum in Candyland? Absolutely not. But in Poker? In Football? Sportscasters often talk about momentum when playing highly competitive games. Whether we’re talking about some kind of charismatic supremacy or simply expert-level play, it’s easy to see when someone starts to take control of a game by gaining momentum, which is a likely sign that we’re looking at a Markovian game.
What about one of my favorite games, Betrayal at House on the Hill? Where does it fall on this Markovian spectrum? After many playthroughs, it feels like a player could gain momentum. They can constantly catch a break, randomly drawing more omens and items than other players while they fail checks and take damage. However, that momentum is merely the result of random chance, not conscious choice. Instead, if we consider that any player at any moment could swap out with a new player without any change at all in strategy or efficiency, we could easily call Betrayal a Markovian game.
What about a game like Dominion? One of the rules of Deckbuilders is that I’m not allowed to look through my deck at any moment, which means that if I arrive mid-game, I can’t know what cards I should buy to keep the deck moving at top efficiency. Deckbuilders are all about building momentum while dealing with imperfect information. Which is tons of fun, but totally not Markovian.
At this point, I just want a test to find out if a game meets these Markovian criteria. So here we go. Let’s make a declarative statement!**
A Markovian Game fulfills both of the following equivalent definitions: 1. Having knowledge of past turns does not increase the optimization of future turns. 2. Momentum cannot be gained during the game, except by random chance.
So what about some of my absolute favorite games? How do they fare against the criteria?
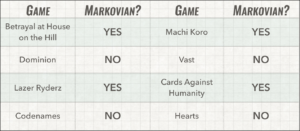
Party Games: I was surprised to apply this idea and find out that not all party games fit this mold! Of course, games like Cards Against Humanity are Markovian, until you start playing with a judge’s preferences in mind. But Codenames is totally not Markovian. Either you’re engaged in the game, hearing all the past clues from both teams as part of your future decision making progress or you’re bad at the game.
The Builders: I already mentioned that deckbuilders aren’t Markovian, but a tableau-builder like Machi Koro absolutely meets these requirements. There’s nothing hidden in Machi Koro. I can look at the cards I’ve previously chosen as well as everyone else’s when I make my next decision. Even a more complex game like Valeria Card Kingdoms doesn’t have a “memory” beyond the state you can see at the start of your turn.
Role-Playing Games: I am clearly a non-Markovian roleplayer. I like to build the kind of story that comes from a table of totally engaged players who are listening to each other and acting as part of a community. But I’ve also sat at tables with players who are on their phone from the moment their turn is over until they start again. They ask the same question almost every time: Who’s still up? The player reads the current state of the game and is usually able to make an effective attack routine because it’s easy to build a D&D character who does the same thing every turn! I shoot the strongest looking person with two arrows. In this sense, there’s even a Markovian playstyle! It isn’t my preferred playstyle, but does it necessarily make the game less effective? I’m not sure I can say.
The Questionables: What about Vast? I love that game, but it is a complex game potentially involving constantly changing deals and alliances. Those are huge giveaways that a game isn’t Markovian at all. If I have to remember how your betrayal when I make my future plans… I guess that means we can cross off every single game with a secret betrayer mechanic from our list.
The Strategies: I am sad to say that Hearts doesn’t make this list. You have to do to much strategizing! Since that is against our definition, I’ll also add every other game where a strategy takes time… you know, since that’s basically exactly how we came up with our description of momentum.
Okay, let’s wrap this monster post up. Why do I care about Markovian games? I’m working up a hypothesis that Markovian Games are easier for new gamers. This might be the key to fixing my holiday game nights forever.
Dear readers, let’s get some data together! Pick some of your favorite games and determine whether or not they meet the Markovian criteria posted above. Then use your experience and think about whether or not those games are good for brand new players. Finally, send me your results at richard@atomicgametheory.com. We need a ton of data from a bunch of different people before even approaching statistical professionalism, so let’s get cracking!