As I’ve probably mentioned before, randomness and probability are highly unintuitive ideas. Not that we can’t understand what they are, but that their natures make it difficult to predict what will happen in specific situations. One great example of probability comes from an idea we call the random path. Imagine a person walking down the street. Before taking a step, they have to spin around until they are facing in a random direction. This erratic motion could lead to a completely chaotic mess with interesting applications to study, but this experiment also has some problems. Motion creates momentum, so our walker might tend towards one direction over another. They might also spin for the same amount of time each step, always turning precisely 270 degrees.
Instead, let’s look at the simplest version of this example: the one dimensional path. We’ll start by setting a meeple on the zero step of a physical number line. For each step, we’ll flip a coin and roll 1d10. If the coin shows heads, we’ll move to the left a number of spaces equal to the d10 roll. If the coin shows tails, we’ll move to the right.
Let’s also attempt to answer the following two questions:
a. Can we predict where the meeple will be after 10 turns?
b. How long does the number line need to be for a 10 turn walk?
So, like any good statistician, I first tried it out. I completed a series of ten experiments and recorded my results. My results varied from 12 on the right to 31 on the left. Seven of my random paths ended on the left, while only three went right. I hadn’t expected any significantly larger numbers, but I was certainly hoping!
I could have instead looked at this mathematically right from the start. D&D players are very aware that the average result of a ten-sided die is 5.5. I could just consider an average roll every turn. We might also expect that in ten coin flips, we might get heads and tails each five times. In that case, our theoretical average result would be to end up right where we started at zero.
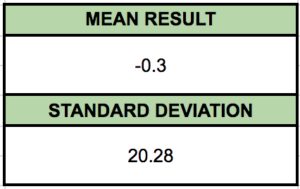
My results are clearly not average, because I never returned a zero! My results weren’t far off, but I need more data to see what’s about to happen. I sent a request out on Twitter and within minutes (Thanks @LtHummus!), I had 1000 additional results and the ability to create as many more as I wanted. What I ended up confirming was one of the most important theories of statistics: given enough results, the experimental mean matches the theoretical. This doesn’t mean I can tell precisely where an individual path will end, but it does give us some place to start.
The second task is significantly more interesting. It feels more likely that we’ll get a result like zero, but the big question is how far does our number line need to stretch. We can see that a result of 100 to the left or right is entirely possible, but it isn’t very likely—in fact, the odds are 1 in 5,120,000,000,000 that the meeple ends up at one of the two extremes! So, how many numbers do we need in our line?
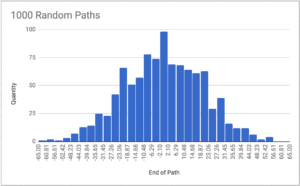Take a look at this data all grouped up. Our experiment forms a simple bell curve! This kind of data is the easiest to analyze. We can see the most of the results are clustered around zero. To talk more mathematically about this clustering, we need to know the standard deviation of our data. The standard deviation measures how grouped our data happens to be. If the standard deviation is small, the data is clumped around the mean. With a large standard deviation, the data is more spread out.
Lucky for us, we’ve got a solid bell curve. In a problem like ours, statisticians know that 68% of all results will lie within one standard deviation of the mean. So 68% of all paths will end somewhere between 20 to the left and 20 to the right. To get 99.7% of all paths in our number line, we only need to get out to 61 on each end! Anything beyond that would be a pretty rare outlier. Even in the 1000 data points I took, none of them fall outside this range.
Overall, our experiment is impossible to predict. Given the random nature of each path, there are just too many possible permutations to consider. However, we can certainly say that it is very likely that the result will end between 61 to the left and right, and we definitely wouldn’t be surprised if it was much closer to zero. Going deeper requires some tougher statistics that we’ll save for another day.
Why in the world am I talking about randomness like this? Because patterns exist in everything. We can look at self-similarity in chaos theory and fractals, but let’s think about where randomness shows up in games. When someone dislikes a game because it is “too random,” often it’s because the final outcome is too hard to predict. A chosen action may not propel someone in the direction they were hoping.
Games involving chance make it clear that specific outcomes are not completely within a player’s control. Clank! isn’t too different from the random path problem. Looking into whether a player will be able to move the right number of spaces involves analyzing their deck and doing a very similar kind of calculation. In this case, rather than rolling 1d10, we’re considering how many cards in the deck have a movement icon.
Cards in Clank! may have icons for Purchasing, Movement, or Fighting enemies. The success and consequences of a player’s actions depend on what happens to be on the cards they draw that turn. They may have an average of one movement a turn, but may instead end up with turns having no movement or other turns with three moves when only one is needed. What we can see from problems like the random path is that if I have 19 cards in my deck and only 4 have a movement icon, the probability that I draw 3 or 4 of them in one turn is very unlikely—but can I get 2? Is that too extreme? All of that leads to the tension that helps make Clank! such an incredible game!
Other games involving randomness include dice games like Zombie Dice and Las Vegas, but also resource gathering games like Catan or Valeria: Card Kingdoms. In each of these games, looking at all the possibilities and paring them down to the realistic probabilities is the key to defeating their internal randomness.